Minimization and Synthesis of the Tail

Link

Consider the unknown component equation $T \circ X \equiv M$, where $T$ and $M$ are given, and $X$ is the unknown. The corresponding architecture is:

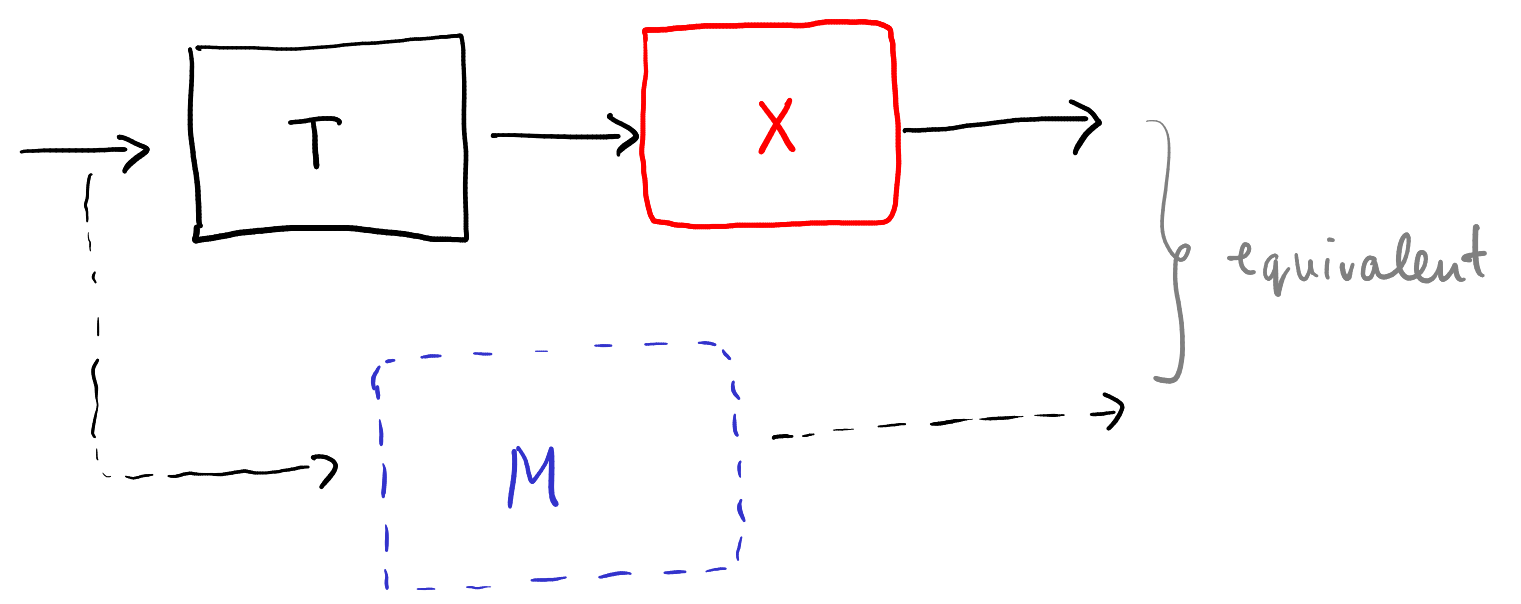
Their results:

• The realisability problem (Problem 4 in paper, called ‘feasibility’) is solveable in poly time.
• The synthesis problem (Problem 3 in paper) is in exp-time hard. They show this by describing problem instances whose all solutions have exp size.
• That is the first time I encounter the case of the complexity gap between realisability and synthesis.
• They also consider the minimization problem where $X$ is given, and the goal is to find the minimal $X$ satisfying the equation. They describe an algorithm of time complexity $2^{poly(|T|\cdot|X|)}$, which is an exponential improvement over previously known 2EXP algorithms.
• Finally, they evaluate their minimization algorithm on examples. They don’t seem to have an implementation of the synthesis algorithm.

Notes:

• Seems related to shield synthesis.
• There is a variant of the ‘unknown component equation’ that uses the language inclusion: $T \circ X \subseteq M$. That is even closer to synthesis.
• They reference a book “The Unknown Component Problem Theory and Applications” that may have interesting expose of the methods.
• They reference a paper “The maximum set of permissible behaviors for FSM networks” which seems important, as they use E-machines mentioned there. They somewhat improve upon that paper, because they refine the complexity for realisability and synthesis.
• For the minimization problem, they improve upon the Kim-Newborn algorithm from paper “The Simplification of Sequential Machines with Input Restrictions”, and avoid the determinization step there.
• Interesting that the ‘head minimization’ problem was solved, and seems easier (paper 2 in references).
• Their proposed specification for the exponentially large solutions might be interesting to SYNTCOMP.