Temporal Stream Logic: Synthesis beyond the Bools
synthesis logic data CEGAR The architecture is:
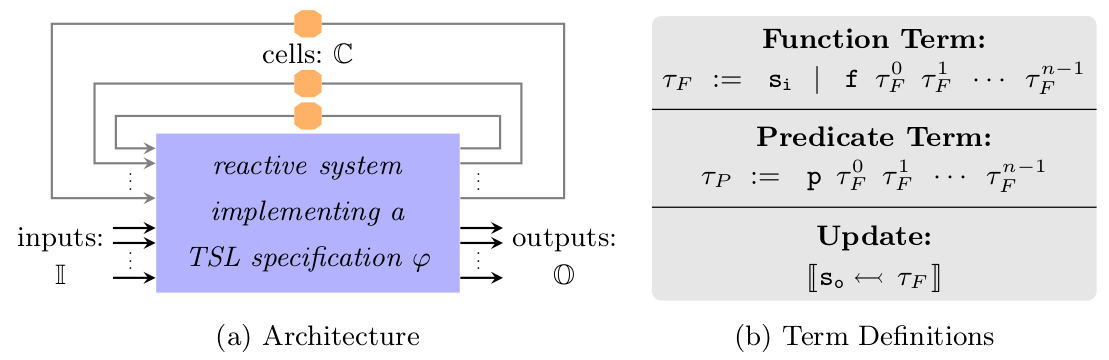
The number of (memory) cells is fixed a-priori.
Inputs and outputs are data, but they all will be treaten syntactically in the synthesis approach.
‘TSL’ specifications contain function and predicate terms, and updates.
You can’t compare data for equality, etc., only what is permitted by the (uninterpreted) predicates.
The grammar of TSL formulas is:
$
\varphi ~~ := ~~ \tau \in Pred \cup Updates ~~ | ~~ \neg \varphi ~~ | ~~ \varphi \wedge \varphi ~~ | ~~ X \varphi ~~ | ~~ \varphi U \varphi
$
Example:

Systems are strategies of the form $PredVals^ * \rightarrow Updates$, where $PredVals$ are valuations of the predicates provided by the environment. For $Updates$, they only allow for having the functional terms that appear in the specification formula, or ‘keep the previous value’. Note that this still allows for having ‘recursion’: a cell can store $func (c)$, thus during the execution it will have $c, func(c), func(func(c)), …$. (Or looks like they allow this.)
Synthesis approach:
- Bound the number of cells and states.
- Treat TSL formula syntactically.
- If the formula is realisable, then the system is correct
- If the formula is unrealisable, then the environment might has been cheating: it could say at moment $m_1$ that $pred(c) \in PredVals$ is true, then later at moment $m_2$ say that $pred(c)$ is false. Note that here $c$ is the same functional term, it could be initial value of a cell, or could be input at the same moment. The important thing is that they need to unfold all possible functional terms. This is possible since the number of system states is fixed a-priori, hence the counterexample’s length is bounded as well (seems like).
- If the environment has been cheating, then the counter-example is spurious and the model checking phase is not over yet. We add a constraint to exclude the counter-example. The constraint is of the form: “if system’s updates are like these, then these two particular predicates should have the same values at moments $m_1$ and $m_2$”.
- I think you could add the constraints on predicate consistency beforehand and avoid the CEGAR refinement, but maybe there are too many such constraints which makes such addition impractical. Mmm, unclear.
Other notes and questions:
- The specification of the music player does not need functional terms, etc.,
and can be encoded using standard Boolean signals:
you only need one Boolean variable to remember the state (they use
Ctrlcell for that) (well, this seems to hold for all their benchmarks in table 1, but (a) you don’t know this beforehand? (b) adding such variables may convolute the spec and dilute the meaning?). - did they solve parameterised benchmarks more efficiently? (e.g., they have a lift, is it parameterised?)
Their results:
- The bounded synthesis approach with CEGAR refinement in the model checking phase (well, in the synthesis phase, but SMT based bounded synthesis is essentially model checking with system functions being unknown). The tool that goes from TSL to Android implementation, seems like a lot of engineering.
- Proof of undecidability of TSL logic (via PCP).
- Benchmarks and experiments. Most benchmarks do not require CEGAR at all, I wonder why they are so easy.