Note on Estimator-Based Reactive Synthesis under Incomplete Information

I was looking for complexity results of computing memory-less strategies under incomplete information, and stumbled upon this paper: Estimator-Based Reactive Synthesis.

The popular practical synthesis method, for GR1 specifications, is PTIME (from now on: wrt. game arena size). In practice we often get incomplete information about the surroundng, for example: a robot may not have a full info about the surrounding, or its sensors may be noisy. Unfortunately, the complexity of the reactive synthesis under incomplete information is EXPTIME, which is often impractical. Can we get PTIME?

In the paper, the authors suggest to lose completeness but gain the PTIME procedure. But the degree of lost completeness is somewhat “manageable” by designers: designers specify what information should be tracked from the surroundings (thus, we use human expertise).

In other words, in the complete (EXPTIME) procedure, we automatically track everything possible. If something can be learned, we learn it. In the proposed procedure, designers restrict what should actually be tracked.

The synthesis procedure is divided into two steps:

1. synthesize a positional estimator
2. synthesize the full system provided the estimator

The following picture is from their paper describes the system we want to synthesize:

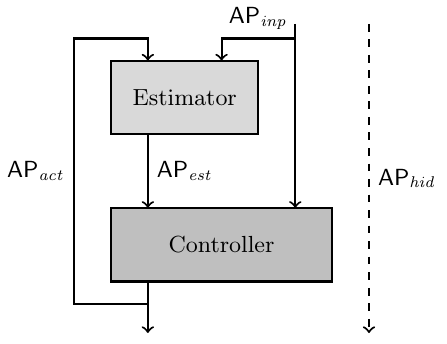
where $inp$, $est$, $act$, and $hid$ are input, esimator, output, and hidden variables.

Now let’s look what are the specs for estimator and controller. In the original approach, when we have only one component (not separated into estimator and controller), we have LTL spec $\varphi(inp, act, hid)$ that talks about $inp$, $act$, and $hid$ variables. In the separated system, we need two specs, one for estimator, and one for controller.

The estimator spec:

• the user has to provide $\rho_e(inp, act, hid)$ – formula over current and next values of variables $inp$, $act$, $hid$. The formula’s intent is to describe assumptions about behaviour of hidden values.

• the user has to provide $\rho_s(inp, act, hid, est)$ – formula over current and next values of $inp$, $act$, $hid$, and $est$. The formula’s intent is to describe what kind of estimations we want to have.

• thus, the estimator spec $EST \models \rho_s(inp,act,hid,est) \ \text{W} \neg \rho_e(inp,act,hid)$

The controller spec: given the original spec $\varphi(inp, act, hid)$ for non-separated components, the new controller spec is $CON \models EST \rightarrow \varphi’(inp, act, est)$, which means that the controller needs to satisfy $\varphi’$ only on runs generated by the estimator. Additionally, $\varphi’$ should be such that $\varphi’(inp, act, est) \land \text{G}\rho_e \land \text{G}\rho_s \rightarrow \varphi(inp, act, hid)$. It is user responsibility to find such $\varphi’$!

Now back to the synthesis steps (1) and (2). Both steps use the synthesis under full information, and are PTIME (the first one uses synthesis for safety specs, the second uses GR1 procedure). Both steps are complete. But..be careful to understand what is a positional estimator! (and that is where we lose completeness) At first, I misuderstood the definition, and did not believe in the completeness (wrt. positional esimators).

Positional Estimators

Here is the definition of an estimator from their paper (definition of the “positional” follows):

Where $\rho_e=\rho_e(obs,hid)$ and $\rho_s=\rho_s(obs,hid,est)$. Note that $\rho_e \rightarrow_s \rho_s$ means $\rho_s W \neg \rho_e$. Intuitively, an estimator should satisfy the safety-like spec and be independent of hidden values.

Now comes the interesting part:

Important note:

• when gluing sequences of hidden valuations, the values of hidden variables may jump at the “mixing point”! But the positional estimator should tolerate such jumps, and still satisfy $\rho_s$. I don’t have an intuition for that yet (does this imply that hidden values can jump all the time?¹)

Finally, to the positonal estimators:

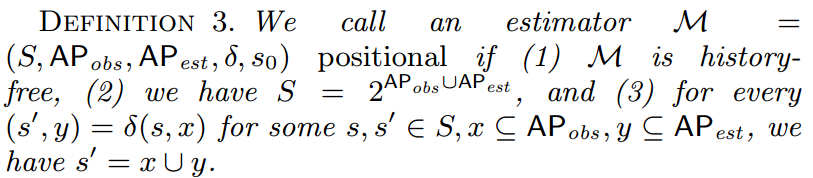
Let’s spend some time with def 3. State space of the positional estimator consists of pairs $(act,inp,est)$ (where $obs = (inp,act)$). Later, we synthesize an estimator using two phases. First, compute set $R$ of reachable states that satisfy $(\rho_e,\rho_s)$. Second, compute the transition relation $\rho_u$ of the positional estimator as: \(\rho_u = \{ ((o,e),(o',e')) \in Obs \times Est \ | \ \forall h,h':\\ (o,e,h) \in R \land ((o,h),(o',h')) \in \rho_e \rightarrow ((o,e,h),(o',e',h')) \in \rho_s\}\)

Intuitively: the game arena when synthesizing estimators is $Obs\times Est \times Hid$, but positional estimators can depend only on $Obs \times Est$ (and don’t have any other memory). Thus, their strategy should abstract away $Hid$. To do so, we remove from estimator transition relation $\rho_u$ any transiton $(o,e) \rightarrow (o’,e’)$ that can have $h,h’$ with $((o,e,h), (o’,e’,h’)) \models \rho_e \land \neg \rho_s$.

Proof of Completeness

The proof of completeness of the first step (synthesis of positional estimators) uses the “important note” we saw before. I put it here, but be careful, it might be junk.

Computing positional estimators via rho_u is complete.
>>
Suppose we miss a PE strategy.
⇔
there is a PE strategy, but it is not included into rho_u
⇔
at least one of its moves is not included into rho_u

thus, let (o,e)->(o',e') \not\in rho_u
⇔
either
(a)      ∀h:¬R(o,e,h) or
(b)  ∃h1,h2: R(o,e,h1) &
             (o,e,h1)->(o',e',h2) |= ¬(rho_e->rho_s)

(a) is not possible
(b) consider R(o,e,h1) & (o,e,h1)->(o',e',h2) |= ¬(rho_e->rho_s)
    ⇔
    R(o,e,h1) & (o,e,h1)->(o',e',h2) |= rho_e & ¬rho_s

    If use the original strategy, is R(o,e,h1)=true?
    1. R(o,e,h1)=true
       Acc. def1 ("seq of hidden values does not affect strategy's truth of rho_e->rho_s"):
         (o,e,h1)->(o',e',h2) |= rho_e -> rho_s,
       but we know that (o,e,h1)->(o',e',h2) |= rho_e & ¬rho_s
       ϟ

    2. R(o,e,h1)=false
       It is not possible to reach (o,e,h1) if play acc. the original strategy.
       But there is h` s.t. (o,e,h`) is reachable if play acc. the original strategy [^1].
       Let r` be the sequence of hidden values with which (o,e,h`) is reachable (at moment i`):
         r` = r`_0...r`_i`... where r`_i`=h`
       We also know for h1 and h2:
         R(o,e,h1) & (o,e,h1)->(o',e',h2) |= rho_e & ¬rho_s
       Let r be the sequence of hidden values with which (o,e,h1) is reachable (at moment i),
       followed by (o,e,h2) at moment {i+1}.
       Acc. def2 PE strategy should satisfy rho_s if plaid on the composed sequence
         r`_0...r`_{i-1}` r_i r_{i+1}
       Consider the transition on (r_i,r_{i+1}):
         acc. the original strategy we play (o,e)->(o',e')
         ⇔
         (o,e,r_i) -> (o',e',r_{i+1})
         ⇔
         (o,e,h1) -> (o',e',h2)
       Acc. def2, since our strategy is PE, (o,e,h1)->(o',e',h2) should satisfy rho_s,
       but we know that
         R(o,e,h1) & (o,e,h1)->(o',e',h2) |= rho_e & ¬rho_s
       ϟ
⇔
the assumption (that we miss a PE strategy) is false.

Proof Footnotes:
[^1]:  in the beginning, we should consider only such (o,e)->(o',e')..
<<

Footnotes